Contoh Soal Usaha dan Energi Serta Pembahasannya

18 Juli 2016:

• waktu publish
• menambahkan 23 soal

10 April 2022:

• redirect ke permalink baru
• update persamaan ke mathjax
• mengkoreksi ulang pembahasan soal
• update format QDL, banyaknya soal: easy (5), medium (8), hard (10)

Daftar isi

• 1 Question Difficulty Level: Easy
• 2 Question Difficulty Level: Medium
• 3 Question Difficulty Level: Hard

Buka semua pembahasan Tutup semua pembahasan

Mode try out (masih tahap perkembangan, hanya menampilkan waktu)

02:00:00

Mulai Try Out!

Question Difficulty Level: Easy

Soal No. 1
Bila hukum kekekalan energi mekanik untuk sistem berlaku maka ...
A. Energi kinetik sistem selalu berkurang
B. Energi potensial sistem selalu bertambah
C. Jumlah energi potensial dan energi kinetik sistem selalu berkurang
D. Jumlah energi potensial dan energi kinetik sistem selalu bertambah
E. Jumlah energi potensial dan energi kinetik sistem adalah tetap

Pembahasan:

Energi mekanik adalah jumlah energi potensial dan energi kinetik
Energi mekanik untuk sistem selalu tetap atau kekal
Jawaban: E

Soal No. 2
Sebuah mobil melakukan kerja (usaha) sebesar 800.000 joule untuk menempuh jarak 1 km dengan kelajuan tetap. Besar gaya yang dilakukan mobil itu adalah ...
A. 200 N
B. 500 N
C. 600 N
D. 800 N
E. 1500 N

Pembahasan:

$\begin{aligned} W &= \vec{F}\cdot \vec{s}\\ 800.\hspace{-.2em}\cancel{000} &= F\cdot 1\hspace{-.2em} \cancel{000}\\ F &= 800\ \mathrm{N} \end{aligned}$

Jawaban: D

Soal No. 3
Seorang anak menarik benda bermassa 1 kg dengan gaya 40 N dengan sepotong tali dan membentuk sudut 60°.

Usaha yang dilakukan anak tersebut untuk memindahkan benda sejauh 4 meter adalah ...
A. 60 J
B. 65 J
C. 70 J
D. 75 J
E. 80 J

Pembahasan:

$\begin{aligned} W&= \color{red}{\vec{F}}\cdot\vec{s}\\ W&= \color{red}{F}s\color{red}{\cos\theta}\\ &=40\cdot 4\cdot \cos{60{}^{\circ}}\\ &=160\cdot 1/2\\ &=\mathrm{80\ J} \end{aligned}$

Jawaban: E

Soal No. 4
Sebuah bola bermassa 2 kg dijatuhkan tanpa kecepatan awal dari atas gedung melewati jendela A di lantai atas ke jendela B di lantai bawah dengan beda tinggi 5,5 m (g = 10 m/s²). Besar usaha untuk perpindahan bola dari jendela A ke jendela B adalah ...
A. 100 J
B. 110 J
C. 120 J
D. 130 J
E. 140 J

Pembahasan:

$\begin{aligned} W &= \Delta E_p\\ &= m\cdot g \cdot \Delta h\\ &= m\cdot g \cdot (h_2-h_1)\\ &= 2\cdot 10 \cdot (5,5)\\ &= 110\ \mathrm{J} \end{aligned}$

Jawaban: B

Soal No. 5
Sebuah peti yang massanya 80 kg dinaikkan dari tanah ke atas truk yang tingginya 1,5 meter. Bila percepatan gravitasi bumi 10 m/s². maka besar usaha yang harus dikeluarkan adalah ...
A. 1200 J
B. 1100 J
C. 1000 J
D. 800 J
E. 600 J

Pembahasan:

$\begin{aligned} W &= \Delta E_p\\ &= m\cdot g \cdot \Delta h\\ &= m\cdot g \cdot (h_2-h_1)\\ &= 80\cdot 10 \cdot (1,5)\\ &= 1200\ \mathrm{J} \end{aligned}$

Jawaban: A. 1200 J

Rekomendasi Artikel lain:

• Soal Gaya Gravitasi
• Soal Impuls dan Momentum
• Soal Hukum Hooke

Question Difficulty Level: Medium

Soal No. 1
Sebuah peluru ditembakkan dengan kecepatan awal 40 m/s dan sudut elevasi 37° (tan 37° = 3/4). Jika massa peluru 0,01 kg maka usaha oleh gaya gravitasi pada peluru sejak ditembakkan sampai jatuh ke tanah kembali sebesar (g = 9,8 m/s²) adalah ...
A. 100 J
B. 40 J
C. 20 J
D. 10 J
E. 0 J

Pembahasan:

Hati-hati jebakan, yang ditanyakan adalah usaha oleh gaya gravitasi pada peluru sejak ditembakkan sampai jatuh ke tanah kembali.

$\begin{aligned} W &= Fs \cos \theta\\ &= F_{\mathrm{grav}} \cdot s \cdot \cos 90{}^{\circ}\\ &= F_{\mathrm{grav}} \cdot s \cdot 0\\ &= 0 \end{aligned}$

Jawaban: E

Soal No. 2
Usaha yang dilakukan terhadap benda bermassa 1 kg agar berpindah sejauh 1 meter adalah W joule. Besar usaha yang dibutuhkan untuk memindahkan benda sejauh 0,5 meter yang massanya 2 kg adalah ...
A, 0,25 W
B. 0,5 W
C. W
D. 2 W
E. 4 W

Pembahasan:

Persamaan untuk usaha adalah

$\begin{aligned} W = Fs \cos \theta \end{aligned}$

Misal kita asumsikan $F$ memiliki besar yang sama, maka:

$\begin{aligned} &W \sim s\ \mathrm{(berbanding\ lurus)}\\[0.5em] &\frac{W_2}{W_1}=\frac{s_2}{s_1}\\[0.5em] &\frac{W_2}{W_1}=\frac{0,5}{1}\\[0.5em] &W_2=0,5W_1 \end{aligned}$

Jawaban: B

Soal No. 3
Energi 4.900 J digunakan untuk mengangkat vertikal benda bermassa 50 kg. Benda akan naik setinggi ... m (g = 9,8 m/s²)
A. 0,1
B. 10
C. 98
D. 245
E. 960

Pembahasan:

$\begin{aligned} W &= \Delta E_p\\ 4900 &= m\cdot g\cdot \Delta h\\ 4900 &= 50\cdot 9,8\cdot \Delta h\\ \Delta h &= 10 \end{aligned}$

Jawaban: B

Soal No. 4
Sebuah meja massanya 14 kg mula-mula diam diatas lantai licin, didorong selama 4 sekon bergerak lurus dengan percepatan 2 m/s². Besar usaha yang terjadi adalah ...
A. 440 J
B. 448 J
C. 496 J
D. 504 J
E. 602 J

Pembahasan:

Usaha yang terjadi pada benda tersebut melibatkan energi kinetik, melalui hubungan $W = \Delta E_k$, untuk mencari energi kinetik ini kita membutuhkan kecepatan akhir dan awal dari benda. Benda mula-mula diam, ini artinya $v_0 = 0$. Bagaimana dengan kecepatan akhirnya $(v_t)$?

Perhatikan bahwa pada soal 'benda didorong selama 4 sekon bergerak lurus dengan percepatan 2 m/s' dari sini kita dapat mengetahui kecepatan akhir benda dari persamaan GLBB:

$\begin{aligned} v_t &= v_0 + at\\ &= 0 + 2\cdot 4\\ &= 8\ \mathrm{m/s} \end{aligned}$

sehingga kita dapat memasukkannya ke dalam hubungan persamaan usaha dan energi kinetik berikut ini

$\begin{aligned} W &= \Delta E_k\\ &= (1/2)\cdot m \cdot (v_2^2 - v_1^2)\\ &= (1/2)\cdot 14 \cdot (8^2-0^2)\\ &= 7\cdot 64\\ &= 448\ \mathrm{J} \end{aligned}$

Jawaban: B

Soal No. 5
Sebuah benda bermassa 4 kg, mula-mula diam, kemudian bergerak lurus dengan percepatan 3 m/s². Usaha yang diubah menjadi energi kinetik setelah 2 detik adalah ...
A. 6 J
B. 12 J
C. 24 J
D. 48 J
E. 72 J

Pembahasan:

Untuk mencari usaha yang diubah menjadi energi kinetik dapat dicari melalui hubungan $W=\Delta E_k$, dari soal tersebut kita belum mengetahui kecepatan akhir dari benda. Kita manfaatkan persamaan GLBB berikut ini:

$\begin{aligned} v_t &= v_0 + at\\ &= 0 + 3 \cdot 2\\ &= 6\ \mathrm{m/s} \end{aligned}$

karena kita telah mengetahui kecepatan akhirnya, kita dapat menggunakan hubungan usaha dan energi kinetik berikut ini:

$\begin{aligned} W &= \Delta E_k\\ &= (1/2) \cdot m \cdot (v_2^2-v_1^2)\\ &= (1/2) \cdot 4 \cdot (6^2-0^2)\\ &= 72\ \mathrm{J} \end{aligned}$

Jawaban: E

Soal No. 6
Sebuah mobil yang massanya 250 kg mula-mula diam bergerak di jalan raya dengan kecepatan 20 m/s. Jika gaya gesekkan mobil dengan jalan 100 N dan mobil telah bergerak sejauh 50 m. Gaya yang dikerjakan oleh mesin mobil tersebut adalah ...
A. 900 N
B. 1000 N
C. 1100 N
D. 1200 N
E. 1300 N

Pembahasan:

Gaya yang dikerjakan oleh mesin mobil dapat dicari tahu menggunakan Hukum Newton II, yaitu $\sum F=ma$. Namun, kita belum mengetahui berapa percepatan dari mobil tersebut. Mari kita gunakan persamaan GLBB untuk mencari tahu percepatan mobil tersebut,

$\begin{aligned} v_t^2 &= v_0^2 + 2as\\ 20^2 &= 0^2 + 2a\cdot 50\\ 400 &= 100a\\ a &= 4\ \mathrm{m/s^2} \end{aligned}$

selanjutnya hasil ini dapat kita proses dengan menggunakan Hukum Newton II yang di dalamnya melibatkan gaya gesek yang berlawanan arah dengan arah gerak dari mobil tersebut. Misal arah kanan positif: arah $F$ dan $a$, dan arah kiri negatif: arah $f_{gesek}$. Berikut ini adalah penyelesaiannya:

$\begin{aligned} \sum F &= ma\\ F-f_{gesek} &= ma\\ F-100 &= 250\cdot 4\\ F &= 1100\ \mathrm{N} \end{aligned}$

Jawaban: C

Soal No. 7
Benda bermassa 1 kg dilempar vertikal ke atas dengan kecepatan awal 40 m/s. Jika percepatan gravitasi bumi 10 m/s², besar energi kinetik benda saat berada pada ketinggian 20 m adalah ...
A. 300 J
B. 400 J
C. 500 J
D. 600 J
E. 700 J

Pembahasan:

Sebenarnya soalnya ini agak rancu, karena ketinggian awal dari benda bisa berapa saja. Untuk mengerjakan soal ini, saya asumsikan ketinggian awal benda $(h_0)$ adalah 0 meter. Selanjutnya dapat kita proses menggunakan Hukum kekekalan energi mekanik:

$\begin{aligned} EM_t &= EM_0\\ Ek_t + Ep_t &= Ek_0 + Ep_0\\ Ek_t + mgh_t &= (1/2) m v_0^2 + mgh_0\\ Ek_t &= (1/2)mv_0^2 + mg(h_0-h_t)\\ &= (1/2)\cdot 1 \cdot 40^2+ 1\cdot 10\cdot(0-20)\\ &= 800 - 200\\ &= 600\ \mathrm{J} \end{aligned}$

Jawaban: D

Soal No. 8
Dengan menggunakan tangga, seseorang membawa beban 20 kg setinggi 3 m dalam waktu 25 sekon. Jika g = 10 m/s² maka daya rata-rata yang diperlukan orang itu adalah ...
A. 12 watt
B. 24 watt
C. 30 watt
D. 120 watt
E. 300 watt

Pembahasan:

$\begin{aligned} P &= \frac{W}{t} = \frac{\Delta E}{t} = \frac{\Delta E_k + \Delta E_p}{t} = \frac{0 + \Delta E_p}{t}\\[0.5em] &= \frac{\Delta Ep}{t}\\[0.5em] &= \frac{mg(h_2-h_1)}{t}\\[0.5em] &= \frac{20\cdot 10 \cdot (3-0)}{25}\\[0.5em] &= 24\ \mathrm{watt} \end{aligned}$

Jawaban: B

Question Difficulty Level: Hard

Soal No. 1
Sebuah mobil bermassa M mempunyai mesin berdaya P. Kecepatan yang bisa dicapai dari keadaan diam dalam waktu 2 s adalah ...
A. $4\ P/M$
B. $\sqrt{2P/M}$
C. $2\sqrt{P/M}$
D. $2\ P/M$
E. $4\ PM$

Pembahasan:

$\begin{aligned} P &= \frac{W}{t} = \frac{\Delta E}{t} = \frac{\Delta E_k + \Delta E_p}{t} = \frac{\Delta E_k + 0}{t}\\[0.5em] P &= \frac{\Delta E_k}{t}\\[0.5em] P &= \frac{(1/2)M(v_t^2-v_0^2)}{t}\\[0.5em] P &= \frac{(1/2)M(v_t^2-0^2)}{2}\\[0.5em] v_t^2 &=4P/M\\[0.5em] v_t &= 2\sqrt{P/M} \end{aligned}$

Jawaban: C

Soal No. 2
Sebuah benda bermassa 20 kg terletak pada bidang miring dengan sudut 30° terhadap bidang horizontal. Jika percepatan 9,8 m/s² dan benda bergeser sejauh 3 meter ke arah bawah, usaha yang dilakukan oleh gaya berat adalah ...

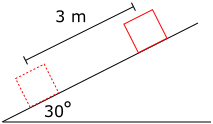A. 60 J
B. 65,3 J
C. 294 J
D. 300 J
E. 588 J

Pembahasan:

Mari kita gambar terlebih dahulu diagram bebasnya:

Dapat dilihat pada gambar di atas bahwa gaya berat $Z$ memiliki vektor perpindahan ke arah bawah sebesar $mg\sin \theta$ sehingga

$\begin{aligned} W &= F_Z\cdot \Delta s\\ W &= mg\sin \theta\ \Delta s\\ W &= 20\cdot 9.8 \cdot \sin 30^{\circ} \cdot 3\\ W &= 294\ \mathrm{J} \end{aligned}$

Jawaban: C

Soal No. 3
Balok seberat 40 N, meluncur diatas bidang datar yang licin dengan laju 2 m/s. Balok berhenti setelah menekan pegas yang menghadangnya. Jika konstanta pegas 100 N/m, berapa jauh pegas tertekan oleh balok? (g = 10 m/s²)
A. 0,2 m
B. 0,3 m
C. 0,4 m
D. 0,5 m
E. 0,6 m

Pembahasan:

Pertama-tama mari kita cari dahulu massanya:

$\begin{aligned} W &= 40\ \mathrm{N}\\ mg &= 40\\ m\cdot 10 &= 40\\ m &= 4\ \mathrm{kg} \end{aligned}$

Kemudian kita gunakan Hukum kekekalan energi mekanik, dimana:
Keadaan (I): balok akan menekan pegas $(E_k \neq 0, E_{p\ pegas} = 0)$
Keadaan (II): balok menekan pegas dan berhenti $(E_k = 0, E_{p\ pegas} \neq 0)$

$\begin{aligned} EM_t &= EM_0\\ Ek_t + Ep_t &= Ek_0 + Ep_0\\ Ek_t - Ek_0 &= Ep_0 - Ep_t\\ \cancel{(1/2)}m(v_t^2-v_0^2) &= \cancel{(1/2)}k(x_0^2-x_t^2)\\ 4\cdot(0^2-2^2) &= 100 \cdot (0-x_t^2)\\ -16 &= -100\cdot x_t^2\\[0.5em] x_t^2 &= \frac{4}{25}\\[0.5em] x_t &= 2/5 = 0,4\ \mathrm{m} \end{aligned}$

Jawaban: C

Soal No. 4
Sebuah benda bergerak dengan laju 10 m/s saat mulai melewati suatu bidang kasar dan kemudian benda berhenti setelah menempuh jarak 10 m, koefisien gesek kinetis bidang kasar dengan benda adalah ...
A. 0,2
B. 0,3
C. 0,5
D. 0,6
E. 0,7

Pembahasan:

$\begin{aligned} W &= \Delta E_k \rightarrow (E_p = 0)\\ -F_{gesek} \ \Delta s &= Ek_t - Ek_0\\ -\mu_k N\ \Delta s &= (1/2)m(v_t^2-v_0^2)\\ -\mu_k \cancel{m} g \ \Delta s &= (1/2)\cancel{m}(0^2-v_0^2)\\[0.5em] -\mu_k &= -\frac{v_0^2}{2g\ \Delta s}\\[0.5em] \mu_k &= \frac{\cancel{10^2}}{2\cdot \cancel{10}\cdot \cancel{10}}\\[0.5em] \mu_k &= 0,5 \end{aligned}$

Jawaban: C

Soal No. 5
Sebuah benda bermassa 20 kg diberi gaya F yang arahnya sejajar sumbu x dan besarnya merupakan fungsi perpindahan seperti tertera pada gambar. Jika pada x = 0 benda dalam keadaan diam maka pada x = 7 m, kecepatan benda sama dengan ... m/s

A. 2
B. 4
C. 6
D. 8
E. 10

Pembahasan:

$\begin{aligned} \mathrm{Usaha} &= \mathrm{luas\ di\ bawah\ grafik}\\ W &= \mathrm{luas\ trapesium}\\[0.5em] &= \frac{(7+3)\cdot 8}{2}\\[0.5em] &= 40\ \mathrm{J} \end{aligned}$

Kemudian kita gunakan hubungan persamaan usaha dan energi:

$\begin{aligned} W &= \Delta E_k \rightarrow \Delta E_p = 0\\ W &= (1/2)m(v_t^2-v_0^2)\\ 40 &= (1/2)\cdot 20\cdot(v_t^2-0)\\ v_t^2 &= 4\\ v_t &= 2\ \mathrm{m/s} \end{aligned}$

Jawaban: A

Soal No. 6
Sebuah pompa air dapat menaikkan 15 liter air tiap menit dari sumur yang dalamnya 6 m. Air disemburkan oleh pompa ini dengan kecepatan 8 m/s. Daya pompa tersebut adalah ...
A. 20 W
B. 23 W
C. 25 W
D. 27 W
E. 30 W

Pembahasan:

$\begin{aligned} P &= \frac{W}{t} = \frac{\Delta E}{t} = \frac{\Delta E_k + \Delta E_p}{t}\\[0.5em] &= \frac{(1/2)m(v_t^2-v_0^2) + mg(h_t-h_0)}{t}\\ \mathrm{\color{magenta}{note\hspace{-.2em}:}}&\\ \rho &= \frac{m}{V}\rightarrow m = \rho V\\ V &= 15\ \mathrm{liter} = 15\times 10^{-3}\ \mathrm{m^3}\\ \rho_{air} &= 1000\ \mathrm{kg/m^3}\\ t &= 1\ \mathrm{menit} = 60\ \mathrm{s}\\ \mathrm{\color{magenta}{Jadi\hspace{-.2em}:}}&\\ m &= 1000\cdot 15\times 10^{-3} = 15\ \mathrm{kg}\\ \mathrm{\color{magenta}{masukkan\hspace{-.2em}:}}&\\ P &= \frac{(1/2)\cdot 15\cdot (8^2-0^2) + 15\cdot 10\cdot(6-0)}{60}\\ P &= \frac{480 + 900}{60}\\ P &= 23\ \mathrm{watt} \end{aligned}$

Jawaban: B

Soal No. 7
Sebuah bandul 1 kg diikat dan kemudian digerakkan ke kanan, lihat gambar di bawah!

Bandul mencapai ketinggian maksimum 0,5 m, jika massa tali diabaikan maka laju bandul di titik B adalah ... m/s
A. 1
B. 2
C. 3
D. √10
E. √20

Pembahasan:

$\begin{aligned} EM_A &= EM_B\\ Ek_A + Ep_A &= Ek_B + Ep_B\\ 0 + \cancel{m}gh_A &= (1/2)\cancel{m}v_B^2+0\\ v_B &= \sqrt{2gh_A}\\ &= \sqrt{2\cdot 10\cdot 0,5}\\ &= \sqrt{10}\ \mathrm{m/s} \end{aligned}$

Jawaban: D

Soal No. 8
Air terjun setinggi 20 m digunakan untuk pembangkit listrik tenaga air (PLTA). Setiap detik air mengalir 10 m³. Jika efisiensi generator 55% dan percepatan gravitasi g = 10 m/s² maka daya rata-rata yang dihasilkan ... kwatt
A. 110
B. 1100
C. 2200
D. 2500
E. 5500

Pembahasan:

Kita cari terlebih dahulu massa airnya

$\begin{aligned} \rho &= m/V\\ m &= \rho V =\rho_{air}V = 1000\cdot 10 = 10000\ \mathrm{kg} \end{aligned}$

Kemudian kita cari daya rata-ratanya

$\begin{aligned} P &= \frac{W}{t} = \frac{\Delta E}{t} = \frac{\Delta E_p}{t} \rightarrow E_k=0\\[0.5em] &= \frac{mg\ \Delta h}{t}\\[0.5em] &= \frac{10000\cdot 10\cdot (20-0)}{1}\\[0.5em] &= 2.000.000\ \mathrm{watt} \end{aligned}$

ini adalah generator ideal (efisiensi 100%), sedangkan pada soal efisiensi generator tersebut adalah 55%, sehingga:

$\begin{aligned} P &= 55\%\cdot 2.000.000\\ &= 1.100.000\ \mathrm{watt}\\ &= 1100\ \mathrm{kwatt} \end{aligned}$

Jawaban: B

Soal No. 9
Mesin sebuah mobil mempunyai efisiensi sebesar 40% dan menghasilkan rata-rata 50.000 J kerja mekanik per detik selama operasinya. Daya yang hilang dalam mesin tersebut adalah ...
A. 2 × 10⁴ W
B. 3 × 10⁴ W
C. 7,5 × 10⁴ W
D. 12,5 × 10⁴ W
E. 15 × 10⁴ W

Pembahasan:

Daya yang hilang $(P_{loss})$ dalam mesin dapat dicari dengan mencari selisih antara daya yang masuk $(P_{in})$ dan daya yang keluar $(P_{out})$. Kita cari tahu dulu daya yang masuk dan keluarnya,

$\begin{aligned} P_{in} &= \frac{W}{t} = \frac{50.000}{1} = 50.000\ \mathrm{watt}\\ \\ \eta &= \frac{P_{out}}{P_{in}}\cdot 100\%\\[.5em] 4\hspace{-.2em}\cancel{0\%} &= \frac{P_{out}}{50.00\hspace{-.2em}\cancel{0}}\cdot 1\hspace{-.2em}\cancel{0}\hspace{-.5em}\cancel{0\%}\\[.5em] P_{out} &= 20.000\ \mathrm{watt} \end{aligned}$

sehingga daya yang hilangnya adalah

$\begin{aligned} P_{loss} &= P_{in} - P_{out}\\ &= 50.000 - 20.000\\ &= 30.000\ \mathrm{watt}\\ &= 3\times 10^4 \ \mathrm{watt} \end{aligned}$

Jawaban: B

Soal No. 10
Benda A yang memiliki massa 1 kg dan mula-mula diam meluncur 3 m pada papan licin membentuk sudut 30° dengan bidang datar. Kemudian, benda A menumbuk pegas P yang salah satunya tertancap kuat pada ujung papan. Jika konstanta pegas 900 N/m maka pemendekan maksimum pegas adalah ...
A. 4,9 cm
B. 8,7 cm
C. 10,6 cm
D. 12,9 cm
E. 18,7 cm

Pembahasan:

Kita gambar terlebih dahulu ilustrasi dan diagram bebas dari benda tersebut,

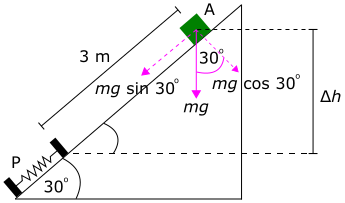Kita gunakan Hukum kekekalan energi mekanik:

$\begin{aligned} Em_t &= Em_0\\ Ep_t + Ep_{p_t} &= Ep_0 + Ep_{p_0}\\ 0 + (1/2)kx_t^2 &= mgh_0 + 0 \end{aligned}$

untuk mencari ketinggian mula-mula, kita dapat menggunakan rumus sinus, yaitu sin θ = depan/miring = Δh/s sehingga didapatkan Δh = h₀ = s sin θ. Kita substitusi ke persamaan terakhir,

$\begin{aligned} (1/2)kx_t^2 &= mgs\sin \theta\\[.5em] x_t^2 &= \frac{2mgs\sin \theta}{k}\\[.5em] x_t^2 &= \frac{2\cdot 1\cdot 10 \cdot 3 \cdot \sin 30^{\circ}}{900}\\[.5em] x_t &= 0,187\ \mathrm{m}\\ x_t &= 18,7\ \mathrm{cm} \end{aligned}$

Jawaban: E