Laporan Praktikum Gerak Lurus Berubah Beraturan

Daftar isi

1. Latar belakang
2. Tujuan Percobaan
3. Dasar Teori
4. Metodologi Percobaan
5. Data dan Analisa
6. Kesimpulan
7. Daftar Pustaka
8. Bagian Pengesahan
9. Lampiran

MENGUKUR KECEPATAN DAN PERCEPATAN RATA-RATA GERAK LURUS SUATU BENDA DENGAN VARIASI JARAK PADA LINEAR AIR TRACK

I. Latar belakang

Dalam kehidupan sehari-hari kita sering menjumpai peristiwa-peristiwa yang berhubungan dengan gerak. Gerak yang dilakukan suatu benda bermacam-macam, contohnya adalah gerak melingkar, gerak lurus, gerak vertikal, gerak parabola, dan lain-lain. Dalam hal ini, gerak yang dikaji adalah tentang pergerakan benda pada gerak lurus. Gerak lurus suatu benda terbagi menjadi 2, yaitu gerak lurus beraturan dan gerak lurus berubah beraturan. Contoh peristiwa gerak lurus berubah beraturan misalnya ketika sebuah bola dilempar lurus ke atas dengan kecepatan tertentu akan mengalami perlambatan saat menuju titik puncak dan akan mengalami percepatan saat bola jatuh menuju titik awal. Kemudian contoh dari gerak lurus beraturan misalnya adalah mobil yang berjalan di lintasan jalan lurus dengan kecepatan tetap (konstan). Dalam kedua peristiwa tersebut dapat diketahui bahwa gerak lurus mempunyai beberapa variabel yang berpengaruh yaitu posisi, perpindahan, kecepatan, dan percepatan. Tetapi dalam peristiwa gerak lurus beraturan, gerak ini sulit terjadi karena benda tersebut pasti mengalami gesekan dengan lintasan, misalnya gesekan antara kaki dengan lantai, ban dengan tanah, dan lain-lain. Dengan adanya gesekan tersebut, seringkali membuat perhitungan atau pengukuran menjadi lebih sulit atau bahkan membuat hasil yang diperoleh jauh dari kesesuaian.

Berdasarkan uraian diatas maka dilakukan suatu percobaan untuk mempelajari gerak lurus dengan menggunakan linear air track. Linear air track adalah suatu alat yang menyediakan lintasan lurus dan mempunyai keunggulan dibandingkan dengan alat-alat praktikum gerak lurus lainnya, yaitu gerakannya yang stabil dan bebas gesekan antara benda dengan lintasannya. Bebas gesekan dari alat linear air track ini karena adanya blower atau air supply yang mendorong benda ke atas, sehingga benda mengambang di atas lintasan. Dengan keunggulan dari alat linear air track dalam hal meminimalkan adanya gaya gesekan maka dilakukanlah percobaan gerak lurus menggunakan linear air track.

II. Tujuan Percobaan

1. Memahami konsep dan percobaan gerak linier satu dimensi
2. Mengukur besar kecepatan v rata-rata dan percepatan a rata-rata suatu benda
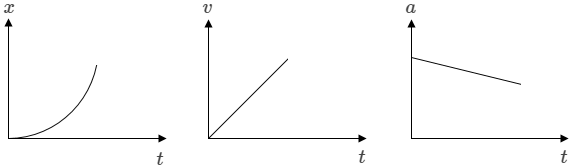
3. Membuat grafik x–t, v–t, dan a–t
4. Mengukur besar percepatan rata-rata dengan menggunakan metode grafik

III. Dasar Teori

Gerak partikel dapat benar-benar diketahui jika posisi partikel setiap saat di dalam ruang diketahui. Posisi partikel adalah lokasi partikel pada suatu kerangka acuan yang kita anggap sebagai titik asal sistem koordinat. Perpindahan partikel didefinisikan sebagai perubahan posisi dalam suatu selang waktu. Ketika berpindah dari posisi awal x_i ke posisi akhir x_f, perpindahan partikel didapat dengan x_f–x_i. Kita gunakan huruf Yunani delta (Δ) untuk melambangkan perubahan nilai. Maka perpindahan atau perubahan posisi partikel dapat ditulis sebagai:

\begin{equation} \Delta x = x_f-x_i \tag{1} \end{equation}

dari definisi ini dapat dilihat bahwa Δx bernilai positif jika x_f lebih besar dari x_i, dan negatif jika x_f lebih kecil dari x_i (Serway, 2014).

Pengukuran posisi, jarak, atau laju harus dibuat dengan mengacu pada suatu kerangka acuan. Ketika berada di atas kereta api yang berjalan dengan laju 80 km/jam, anda mungkin akan memperhatikan seseorang yang berjalan melewati anda ke arah depan kereta dengan laju 5 km/jam. Ini adalah laju orang tersebut terhadap kereta sebagai kerangka acuan. Terhadap permukaan bumi, orang tersebut bergerak dengan laju 80 km/jam + 5 km/jam = 85 km/jam. Penentuan kerangka acuan penting dalam menyatakan kelajuan, tanpa menyadarinya sama sekali kelajuan sering dimaksudkan 'terhadap permukaan bumi' dalam perbincangan sehari-hari. Bahkan jarak pun bergantung pada kerangka acuan. Ketika menspesifikasikan gerak suatu benda, sangat penting untuk tidak hanya menyatakan kelajuannya tetapi juga arah geraknya. (Giancoli, 2001).

Gerak lurus berubah beraturan (GLBB) adalah gerak benda yang memiliki lintasan berbentuk garis lurus, dengan memiliki sifat bahwa jarak yang ditempuh tiap satuan waktu adalah tidak sama besar, sedangkan arah geraknya tetap. Dalam hal ini, jarak yang ditempuh tiap satuan waktu semakin besar atau semakin kecil, maka terjadilah gerak dipercepat atau diperlambat. Jika perubahannya tetap maka disebut gerak lurus berubah beraturan. Contoh gerak lurus dipercepat beraturan adalah gerak jatuh bebas dan gerak vertikal ke bawah (Sarojo, 2014).

Kelajuan rata-rata partikel didefinisikan sebagai perbandingan jarak total yang ditempuh terhadap waktu total yang dibutuhkan:

\begin{equation} v=\frac{\Delta x}{\Delta t} \tag{2} \end{equation}

satuan SI dari kelajuan rata-rata adalah meter per sekon, dan satuan yang lazim di Amerika adalah feet per sekon (ft/s). Kelajuan rata-rata tidak menceritakan apa-apa tentang rincian perjalanan yang dilakukan. Kecepatan dan kelajuan memiliki konsep yang sama, hanya saja untuk kecepatan harus mencangkup arah gerakannya juga. Kecepatan rata-rata partikel didefinisikan sebagai perbandingan antara perpindahan dalam selang waktu Δt = t₂–t₁:

\begin{equation} \bar{v}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1} \tag{3} \end{equation}

Perhatikan bahwa perpindahan dan kecepatan rata-rata dapat bernilai positif atau negatif, bergantung dari apakah x₂ lebih besar atau lebih kecil daripada x₁ (Tipler, 1998).

Ketika kecepatan partikel berubah, partikel dikatakan mengalami percepatan. Untuk gerakan sepanjang sumbu, percepatan rata-rata ā selama interval waktu tertentu Δt adalah:

\begin{equation} \bar{a}=\frac{v_2-v_1}{t_2-t_1}=\frac{\Delta v}{\Delta t} \tag{4} \end{equation}

dimana partikel memiliki kecepatan v₁ pada t₁ dan v₂ pada t₂. Percepatan sesaat (atau percepatan saja) adalah turunan dari kecepatan terhadap waktu:

\begin{equation} a=\frac{dv}{dt} \tag{5} \end{equation}

dengan kata lain, percepatan sebuah partikel pada suatu saat adalah dimana kecepatannya berubah pada saat itu. Secara grafik, percepatan pada suatu titik adalah kemiringan kurva v(t) pada titik tersebut (Halliday, 2010).

IV. Metodologi Percobaan

4.1 Alat dan Bahan

1. Air track berfungsi sebagai lintasan trolly (1 buah)
2. Air supply berfungsi sebagai penyuplai udara agar trolly bergerak mengambang dan mengurangi adanya gesekan (1 buah).
3. Counter berfungsi untuk menghitung interval waktu pergerakan trolly (1 buah).
4. Sensor berfungsi untuk mendeteksi trolly ketika melintas pada air track agar didapatkan interval waktu (2 buah).
5. Dimmer berfungsi untuk mengatur kuat lemahnya hembusan udara dari air supply (1 buah).
6. Trolly berfungsi sebagai objek yang akan diuji pada lintasan air track (1 buah).
7. Magnet berfungsi untuk menahan trolly (1 buah).
8. Control magnet berfungsi untuk mengaktifkan dan menonaktifkan magnet (1 buah).
9. Benang berfungsi untuk menghubungkan antara beban dan trolly (secukupnya).
10. Beban berfungsi sebagai pemberat yang juga menarik trolly agar bergerak (2 buah).
11. Mistar berfungsi untuk memvariasikan jarak antar 2 sensor (1 buah).

4.2 Gambar Rangkaian Alat

—

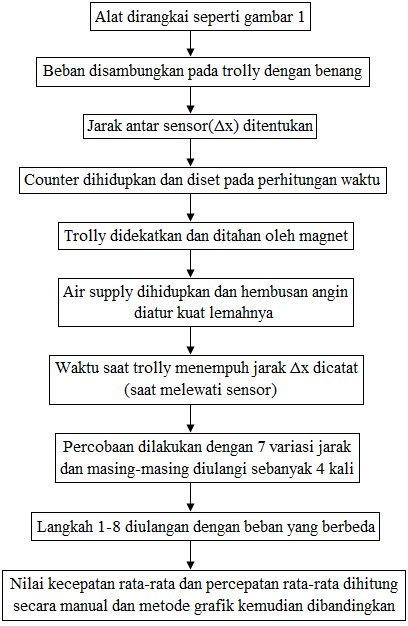
4.3 Langkah Kerja

Gambar 1. Diagram alir prosedur percobaan air track

4.4 Metode Grafik

4.4.1 Grafik 1

Gambar 2. Metode grafik 1 praktikum air track

4.4.2 Grafik 2

Gambar 3. Metode grafik 2 praktikum air track

V. Data dan Analisa

5.1 Data Percobaan

5.2 Analisa Data

Prinsip pada percobaan linear air track ini adalah dengan membuat gerakan trolly atau benda menjadi stabil dan bebas gesekan antara benda dengan lintasannya. Ketika air supply dinyalakan, trolly akan terdorong ke atas dan tertarik oleh beban yang dihubungkan dengan trolly menggunakan benang, sehingga trolly mengambang di atas lintasan. Prinsip ini dilakukan agar benda mengalami gerak lurus berubah beraturan tanpa adanya gaya gesek terhadap lintasan.

Rekomendasi Laporan lain:

• Laporan Pegas
• Laporan Tegangan Permukaan
• Laporan Hukum Ohm

Pada tabel percobaan 5.1.1 dapat dilihat bahwa rata-rata waktu yang didapatkan cenderung lebih besar pada massa beban 20 × 10^-3 kg daripada massa beban 50 × 10^-3 kg, hal ini disebabkan massa beban yang lebih kecil akan menarik trolly dengan gaya kecil juga, sehingga waktu yang diperlukan untuk menempuh jarak tersebut semakin lama atau besar. Dan hal ini juga membuktikan teori impuls bahwa gaya yang diberikan terhadap suatu benda berbanding terbalik terhadap waktu.

Data-data tabel percobaan 5.1.1 digunakan untuk menghitung kecepatan rata-rata benda, percepatan rata-rata benda, dan percepatan sesaat benda secara perhitungan manual dan grafik. Berikut ini adalah gambar grafik hubungan x–t pada massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg:

Gambar 4. Grafik hubungan Δx–Δt pada massa beban 20 × 10^-3 kg

Gambar 5. Grafik hubungan Δx–Δt pada massa beban 50 × 10^-3 kg

Pada grafik x–t massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg terbentuk kurva kuadratik. Kurva pada massa beban 20 × 10^-3 kg agak sedikit melebar kekanan pada arah sumbu x, hal ini menandakan bahwa gambar grafik massa beban 20 × 10^-3 kg memperoleh waktu yang lebih lama daripada massa beban 50 × 10^-3 kg. Jadi, semakin besar massa beban (gaya) maka semakin kecil waktu yang dibutuhkan untuk menempuh lintasan tersebut. Grafik tersebut membentuk kurva karena jarak berbanding lurus dengan kuadrat dari waktu (persamaan garis), sehingga memenuhi persamaan garis y = x² (parabola).

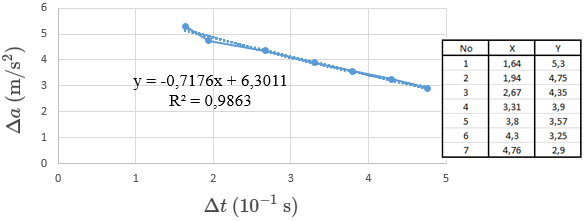
Selain hubungan dari grafik x–t, percobaan ini juga dilakukan untuk mendapatkan grafik dari hubungan percepatan rata-rata terhadap waktu Δa–Δt, berikut ini adalah grafiknya:

Gambar 6. Grafik hubungan Δa–Δt pada massa beban 20 × 10^-3 kg

Gambar 7. Grafik hubungan Δa–Δt pada massa beban 50 × 10^-3 kg

Pada gambar grafik hubungan antara percepatan rata-rata dengan waktu rata-rata di atas, diperoleh kemiringan gradien yang berbeda. Pada gambar grafik massa beban 50 × 10^-3 kg diperoleh gradien yang lebih besar dibanding gambar grafik massa beban 20 × 10^-3 kg. Hal ini menunjukkan bahwa massa beban yang besar (gaya) menimbulkan percepatan yang besar juga. Hal ini bersesuaian dengan Hukum II Newton bahwa gaya berbanding lurus dengan percepatan benda. Jadi semakin besar gaya yang dikerjakan pada benda semakin besar juga percepatan yang dihasilkan. Gambar grafik di atas seharusnya lurus horizontal karena percepatannya konstan akibat dari gaya gesek yang ditiadakan oleh linear air track, tidak miring atau bisa dikatakan nilai gradiennya haruslah nol. Penyebabnya adalah kesalahan-kesalahan yang dilakukan saat percobaan seperti kesalahan dalam pengambilan data atau saat perhitungan, hal inilah yang membuat gambar grafik menjadi miring. Pada perhitungan metode manual pada massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg masing-masing memiliki percepatan rata-rata sebesar 3,49 m/s² dan 3,81 m/s², secara grafik pada massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg masing-masing memiliki percepatan rata-rata sebesar 5,75 m/s² dan 6,5 m/s².

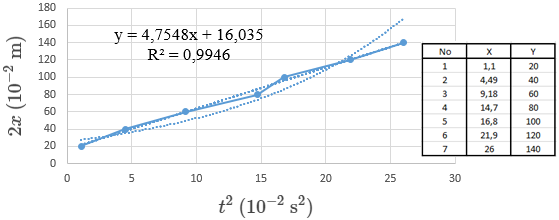
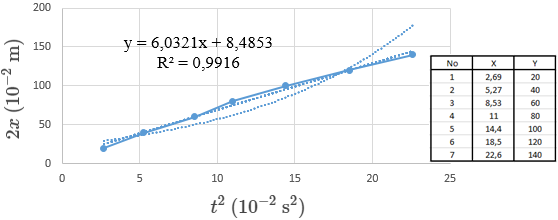
Gambar grafik selanjutnya adalah grafik percepatan sesaat, berikut ini adalah gambar grafik hubungan 2x–t²:

Gambar 8. Grafik hubungan 2x–t² pada massa beban 20 × 10^-3 kg

Gambar 9. Grafik hubungan 2x–t² pada massa beban 50 × 10^-3 kg

Nilai gradien kedua gambar grafik di atas menentukan nilai dari percepatan sesaat, didapatkan nilai dari gradien gambar grafik massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg sebesar (4,76 ± 0,40) m/s² dan nilai dari gambar grafik massa beban 50 × 10^-3 kg sebesar (6,03 ± 0,52) m/s² dengan ketelitian masing-masing beban adalah 99,46% dan 99,10%. Pada perhitungan secara metode manual didapatkan nilai percepatan sesaat dari massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg sebesar 6,92 m/s² dan 7,62 m/s². Nilai dari metode perhitungan secara grafik dan manual ini menunjukkan bahwa percepatan sesaat massa beban 20 × 10^-3 kg lebih kecil dibandingkan dengan massa beban 50 × 10^-3 kg. Hal ini berarti menunjukkan bahwa massa beban (gaya) yang kecil menimbulkan percepatan yang kecil juga. Tidak hanya itu, hasil percobaan tersebut juga telah membuktikan Hukum II Newton yang menyatakan bahwa gaya (massa beban) yang kecil menimbulkan percepatan yang kecil juga, karena gaya berbanding lurus dengan percepatan.

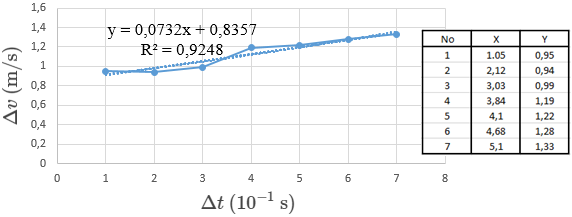
Gambar grafik yang terakhir adalah grafik kecepatan rata-rata, berikut ini adalah gambar grafiknya:

Gambar 10. Grafik hubungan Δv–Δt pada massa beban 20 × 10^-3 kg

Gambar 11. Grafik hubungan Δv–Δt pada massa beban 50 × 10^-3 kg

Pada kedua grafik hubungan Δv–Δt di atas didapatkan nilai dari gradien sama dengan nilai dari kecepatan rata-rata, nilai dari gradien gambar grafik massa beban 20 × 10^-3 kg sebesar (0,073 ± 0,012) m/s dan nilai dari gambar grafik massa beban 50 × 10^-3 kg sebesar (6,032 ± 0,016) m/s dengan ketelitian masing-masing sebesar 92,5% dan 99,1%.

Pada perhitungan secara metode manual didapatkan nilai dari kecepatan rata-rata dari massa beban 20 × 10^-3 kg dan 50 × 10^-3 kg sebesar 1,11 m/s dan 1,16 m/s. Nilai dari metode perhitungan secara grafik dan manual ini menunjukkan bahwa kecepatan rata-rata massa beban 20 × 10^-3 kg lebih kecil dibandingkan dengan massa beban 50 × 10^-3 kg. Hal ini membuktikan bahwa kecepatan rata-rata berbanding lurus dengan gaya, jadi semakin besar gaya yang diberikan semakin besar juga kecepatan rata-ratanya.

VI. Kesimpulan

1. Percobaan gerak lurus satu dimensi dengan menggunakan linear air track ini dapat dipahami sebagai aplikasi dari konsep GLBB karena benda mengalami percepatan yang konstan dan benda tidak mengalami gaya gesekan pada lintasan. Gaya gesek tersebut diminimumkan oleh air supply yang membuat benda (trolly) terdorong ke atas, sehingga benda mengambang di atas lintasan, dan benda bebas gesekan terhadap lintasan. Ketika air supply dinyalakan benda akan tertarik oleh beban yang dihubungkan melalui benang, beban disini bersifat sebagai gaya tarik pada trolly. Ketika trolly melewati sensor 1 dan sensor 2 didapatkan interval waktu yang digunakan untuk menghitung kecepatan rata-rata, percepatan rata-rata, dan sesaat serta masing-masing grafiknya.
2. Kecepatan rata-rata benda dapat dicari dengan menggunakan persamaan Δv = Δx Δt, dan percepatan rata-rata benda dapat dicari dengan persamaan Δa = Δv Δt. Dari data percobaan tabel 5.1.1 didapatkan hasil perhitungan kecepatan rata-rata dan percepatan rata-rata pada beban 20 × 10^-3 kg dan 50 × 10^-3 kg:

1. Kecepatan rata-rata massa beban 20 × 10^-3 kg
   metode perhitungan manual: Δv = 1,11 m/s
2. Kecepatan rata-rata massa beban 50 × 10^-3 kg
   metode perhitungan manual: Δv = 1,16 m/s
3. Percepatan rata-rata massa beban 20 × 10^-3 kg
   metode perhitungan manual: Δa = 6,92 m/s²
4. Percepatan rata-rata massa beban 50 × 10^-3 kg
   metode perhitungan manual: Δa = 7,62 m/s²

1. Grafik hubungan x–t, v–t, dan a–t

1. Pada massa beban 20 × 10^-3 kg
   
   

   Gambar 12. Grafik hubungan x–t, v–t, dan a–t pada massa beban 20 × 10^-3 kg
2. Pada massa beban 50 × 10^-3 kg
   
   

   Gambar 13. Grafik hubungan x–t, v–t, dan a–t pada massa beban 50 × 10^-3 kg

1. Ketika menggunakan metode pada grafik a–t didapatkan nilai dari percepatan rata-rata, yaitu:

1. Massa beban 20 × 10^-3 kg
   metode perhitungan grafik: Δa = (4,76 ± 0,40) m/s²
2. Massa beban 50 × 10^-3 kg
   metode perhitungan grafik: Δa = (6,03 ± 0,52) m/s²

VII. Daftar Pustaka

• Giancoli, D.C., 2001. Fisika Jilid I. Jakarta: Erlangga.
• Halliday, D., 2010. Fisika Dasar Edisi 7 Jilid 1. Jakarta: Erlangga.
• Sarojo, G.A., 2014. Seri Fisika Dasar Mekanika Edisi 5. Jakarta: Salemba Teknika.
• Serway, R.A., 2014. Fisika untuk Sains dan Teknik Edisi 6 Jilid I. Jakarta: Salemba Teknika.
• Tipler, P.A., 1998. Fisika untuk Sains dan Teknik Edisi 3 Jilid I. Jakarta: Erlangga.

VIII. Bagian Pengesahan

—

IX. Lampiran